Bayesian compution with R examples in SAS

学习了oloolo大拿的牛文，上面把 Bayesian compution with R 的例子全部改用sas写了一遍。一面学习oloolo的牛文，一面对照自己写一遍。中途写不出来的回去看看oloolo怎么写的，中间学了不少东西。呵呵，谢谢了。下面把自己尝试的code贴上。

原来作者的R Code:

p = seq(0.05, 0.95, by = 0.1)
prior = c(1, 5.2, 8, 7.2, 4.6, 2.1, 0.7, 0.1, 0, 0)
prior = prior/sum(prior)
data = c(11, 16)
post = pdisc(p, prior, data)
round(cbind(p, prior, post),2)
library(lattice)
PRIOR=data.frame("prior",p,prior)
POST=data.frame("posterior",p,post)
names(PRIOR)=c("Type","P","Probability")
names(POST)=c("Type","P","Probability")
data=rbind(PRIOR,POST)
xyplot(Probability~P|Type,data=data,layout=c(1,2), type="h",lwd=3,col="black")

对应的SAS Code：

options fullstimer formchar='|----|+|---+=|-/\<>*'  formdlim='-'  error=3;
/***************************************************/
/*
模仿oloolo大牛的程序。把 Bayesian compution with R 中的例子用SAS写出来；
原文为oloolo所写；
用来练习，写不出来的，就看看oloolo怎么写的；
哈哈 :)
*/

/*
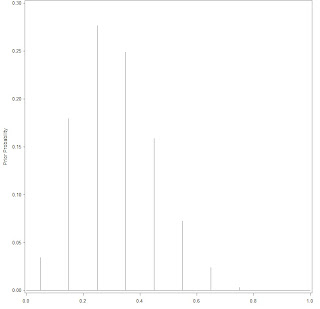
The following is to draw the graph for the discrete prior;
There are ten points that p may take, each with its weight respectively;
*/

data p;
    do p = .05 to .95 by .1;
        output;
    end;
run;


data prior;
input prior @@;
cards;
1  5.2  8  7.2  4.6  2.1  .7  .1  0  0
;
run;


data p;
    retain sum_prior 0;
    do until (eof1);
        set prior end = eof1;
        sum_prior + prior;
    end;
    do until (eof2);
        merge p prior end = eof2;
        prior = prior/sum_prior;
        output;
    end;
    drop sum_prior;
run;

goptions reset = all;
symbol interpol=Needle value=none line=1 color=black;
axis1 label = (angle = 90 'Prior Probability') order = (0 to 0.3 by .05) minor = none;
axis2 label = ('p') order = (0 to 1 by .2) minor = none;
proc gplot data = p;
    plot prior*p / vaxis=axis1 haxis=axis2;
run;
quit;

/*
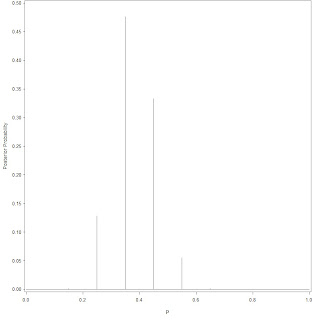
Next is to calculate the posterior and then draw it;
*/

%let n0=16;
%let n1=11;

/*
Calculate the log-likelihood
*/
data p;  
 set p;
 if p > 0 and p < 1 then do;
     log_like = log(p)*&n1 + log(1-p)*&n0;
 end;
 else
     log_like = -999*(p=0)*(&n1 > 0) + (p=1)*(&n0 > 0) ;
run;

/*
Calculate the max(log-likelihood). Since exp(log_likelihood) is very colse to 0, if use it directly, almost all
calculated items is zero. So, use exp(log_likelihood - max), sacle the likelihood. It doesn't change the value
of likelihood since final likelihood = likelihood / sum(likelihood). If both numerator and denominator both
scaled by the same number, it doesn't change the fraction value.
*/
proc means data = p noprint;
    var log_like;
    output out = _max  max(log_like)=max;
run;

data p;
    set _max;
    sum_like = 0;
    do until (eof);
        set p end = eof nobs = ntotal;
        likelihood = exp(log_like - max);
        sum_like + likelihood;
    end;
    do until (eof1);
        set p end = eof1;
        likelihood = exp(log_like - max)/sum_like;
        posterior = likelihood * prior;
        output;
    end;
run;

data p;
    sum_post = 0;
    do until (eof);
        set p end = eof;
        sum_post + posterior;
    end;
    do until (eof2);
        set p end =  eof2;
        posterior = posterior / sum_post;
        output;
    end;
run;

goptions reset = all;
symbol interpol=Needle value=none line=1 color=black;
axis1 label = (angle = 90 'Posterior Probability') order = (0 to 0.5 by .05) minor = none;
axis2 label = ('p') order = (0 to 1 by .2) minor = none;
proc gplot data = p;
plot posterior*p / vaxis=axis1 haxis=axis2;
run;
quit;

data set match merge, an example to study zz

The original post want to match merge A and B, and then got the result as below:

X   Y         Z               flag
1   red      brown       0
1   red      red            1
1   blue     brown       0
1   blue     red            0
3   yellow  red            0
3   yellow  pink           0
3   green   red            0
3   green   pink           0

In proc sql, it's not difficult to use inner join to merge A and B conditional on a.x = b.x. And we need to assign value to flag as if a.y matched by b.z.  At last the program can be down as:

data a;
 input x y $;
 cards;
 1 red
 1 blue
 3 yellow
 3 green
 ;
run;

data b;
 input x z $;
 cards;
 1 brown
 1 red
 2 yellow
 3 red
 3 pink
 ;
run;

proc sql;
   select a.x, a.y, b.z, case when a.y = b.z then 1 else 0 end as flag 
   from a, b
   where a.x=b.x;
quit;

***************************************************************************

 Somebody gives the solution with data step. It's pretty good, as following:

 data c;
 set a;
 do i = 1 to num;
  set b(rename = (x = x2)) nobs = num point = i;
  output;
 end;
run;

data want (drop = x2);
 set c;
 if y = z then flag = 1;
 else flag = 0;
 where x = x2;
run;

To make it clearer, here, the print of data set c is:

                                 Obs    x    y         x2    z

                                    1    1    red        1    brown
                                    2    1    red        1    red
                                    3    1    red        2    yellow
                                    4    1    red        3    red
                                    5    1    red        3    pink
                                    6    1    blue       1    brown
                                    7    1    blue       1    red
                                    8    1    blue       2    yellow
                                    9    1    blue       3    red
                                   10    1    blue       3    pink
                                   11    3    yellow     1    brown
                                   12    3    yellow     1    red
                                   13    3    yellow     2    yellow
                                   14    3    yellow     3    red
                                   15    3    yellow     3    pink
                                   16    3    green      1    brown
                                   17    3    green      1    red
                                   18    3    green      2    yellow
                                   19    3    green      3    red
                                   20    3    green      3    pink

How to draw Normal density in SAS

/* Here we will use function PDF('NORMAL', x, mu, sigma) to get pdf

   More details about this function:

   http://support.sas.com/documentation/cdl/en/lrdict/64316/HTML/default/viewer.htm#a000270634.htm

*/

%let a1=1;

%let b1=1;

%let a2=-1;

%let b2=1;

%let a3=0;

%let b3=1;

data pdf;

      do i=-5 to 5 by 0.02;

   pdf1=pdf('Normal', i, &a1, &b1);

   pdf2=pdf('Normal', i, &a2, &b2);

   pdf3=pdf('Normal', i, &a3, &b3);

   output;

   end;

run;

proc print data=pdf;

run;

goptions reset=all;

symbol1 interpol=j  color=red  width=1  value=none;

symbol2 interpol=j  color=blue width=2  value=none;

symbol3 interpol=j  color=gree width=3  value=none;

axis1   label=(angle=90  'Density')  order=(0 to .5 by .1) minor=none;

axis2   label=('i')      order=(-5 to 5 by 1)  minor=none;;

legend label=none   position=(top right inside)  mode=share;

proc gplot data=pdf;

      plot   pdf1*i  pdf2*i  pdf3*i /overlay 

                                      vaxis=axis1 

                                      haxis=axis2 

                                      legend=legend;

run;quit;