cat("\014")
rm(list=ls())
rpvdata<-read.csv("D:\\SkyDrive\\Public\\landing_page_rpv\\landing_page_rpv.csv",header=T, skip=2)
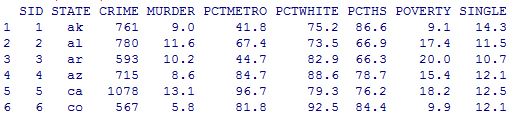
head(rpvdata)
names(rpvdata)<-tolower(names(rpvdata))
rpvdata=rpvdata[rpvdata$product_count>0,]
sapply(rpvdata, class)
str(rpvdata)
rpvdata$lprpv=rpvdata$projected_rpv
attach(rpvdata)
library(ggplot2)
p<-ggplot(rpvdata, mapping=aes(x=lprpv, y=actrpv))
p+geom_point()+stat_smooth()
plot(lprpv, actrpv, col="blue", main="plot of lprpv vs actrpv")

It does not show any clear relation between these two variables from the graph above.
To make it a little clear, the data are grouped into 20 groups based on the percentiles of lprpv(5%, 10%, ..., 100%). And calculate t he weighted mean at each group weighted by variable visits_wt. It is shown the average of lprpv and average of actrpv are somehow linear related.
## bucket data into 20 buckets like sas proc rank did
lprpv_rank<-cut(lprpv, breaks=quantile(lprpv, probs=c(0:20/20)), labels=0:19, include.lowest=T, right=F)
table(lprpv_rank)
## calculate mean of lprpv in each lprpv_rank
tapply(lprpv, lprpv_rank, mean)
## calculate weighted mean
library(plyr)
df_wtm<-as.data.frame(cbind(lprpv, actrpv, lprpv_rank, visits_wt))
lprpv_m<-ddply(df_wtm, .(lprpv_rank), function(x) data.frame(lprpv_mean=weighted.mean(x$lprpv, x$visits_wt)))
actrpv_m<-ddply(df_wtm, .(lprpv_rank), function(x) data.frame(actrpv_mean=weighted.mean(x$actrpv, x$visits_wt)))
overall_wt_m<-merge(lprpv_m, actrpv_m, by="lprpv_rank")
## plot of the data with smoothed curve
ggplot(overall_wt_m, aes(x=lprpv_mean, y=actrpv_mean))+geom_point()+stat_smooth()
## linear regression without product_count information
summary(lm(actrpv_mean ~ lprpv_mean, data=overall_wt_m))

From the graph above, it shows a linear relation if we ignore the first several points with low value of lprpv_mean.
The linear regression result is given below. The adjusted R square is about .3936, which means the regression is not good. Usually R^2 > .8 means the regression is good.

Next we involve another variable called product_count, which is the numer of products on each page. If it is 1, means there is only 1 product on that page. In this condition, we should expect lprpv and actrpv are closely related.
### next include prod_cnt_flag in the analysis
## generate flag variables like sas format did
cutf=function(x) cut(x, breaks=quantile(x, probs=c(0:20/20)), labels=0:19, include.lowest=T, right=F)
prod_cnt_flag<-ifelse(product_count==0, 0, ifelse(product_count==1,1,ifelse(product_count==2,2,ifelse(product_count==3,3,4))))
overall_m=list()
for (i in 1:4){
lprpv_rank<-cut(lprpv[product_count==i], breaks=quantile(lprpv[product_count==i], probs=c(0:20/20)), labels=0:19, include.lowest=T, right=F)
df_wtm<-as.data.frame(cbind(lprpv=lprpv[product_count==i], actrpv=actrpv[product_count==i], lprpv_rank, visits_wt=visits_wt[product_count==i]))
lprpv_m<-ddply(df_wtm, .(lprpv_rank), function(x) data.frame(lprpv_mean=weighted.mean(x$lprpv, x$visits_wt)))
actrpv_m<-ddply(df_wtm, .(lprpv_rank), function(x) data.frame(actrpv_mean=weighted.mean(x$actrpv, x$visits_wt)))
overall_wt_m<-merge(lprpv_m, actrpv_m, by="lprpv_rank")
overall_wt_m=data.frame(cbind(overall_wt_m, prod_cnt_group=i))
overall_m[[i]]=overall_wt_m
}
## or plot with ggplot2, concatenate the list to a long data frame
df=as.data.frame(do.call(rbind, overall_m))
library(ggplot2)
p<-ggplot(df, mapping=aes(lprpv_mean, actrpv_mean))
p+geom_point()+stat_smooth()+facet_wrap(~prod_cnt_group, ncol=1)

Now the data in the first group(top one) is more linear then before as is explained. For the other three groups they also linearly perform better than without group condition.
From this study, we should put the variable prod_cnt_group in the regression as a categorival variable. It will help to improve the model fitting.
key point: 1)how to calculate weighted mean 2)how to aggregate in each level of a factor, this can be done by tapply. But here is done by library(plyr). 3)how to draw separately for each factor level in ggplot2 with facet_wrap.